BCK algebra
In mathematics, BCI and BCK algebras are algebraic structures, introduced by Y. Imai, K. Iséki and S. Tanaka in 1966, that describe fragments of the propositional calculus involving implication known as BCI and BCK logics.
Contents |
Definition
BCI algebra
An algebra 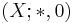 of type
of type 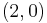 is called a BCI-algebra if, for any
is called a BCI-algebra if, for any 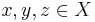 , it satisfies the following conditions:
, it satisfies the following conditions:
- BCI-1
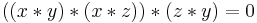
- BCI-2
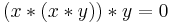
- BCI-3
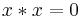
- BCI-4
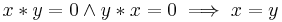
- BCI-5
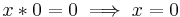
BCK algebra
A BCI-algebra 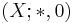 is called a BCK-algebra if it satisfies the following condition:
is called a BCK-algebra if it satisfies the following condition:
- BCK-1
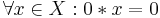
Examples
Every abelian group of is a BCI-algebra, with * group subtraction and 0 the group identity.
The subsets of a set form a BCK-algebra, where A*B is the difference A\B (elements in A but not in B), and 0 is the empty set.
A Boolean algebra is a BCK algebra if A*B is defined to be A∧¬B (A does not imply B).
References
- Angell, R. B. (1970), "Review of several papers on BCI, BCK-Algebras", The Journal of Symbolic Logic 35 (3): 465–466, ISSN 0022-4812, http://links.jstor.org/sici?sici=0022-4812%28197009%2935%3A3%3C465%3AAARWAP%3E2.0.CO%3B2-C
- Arai, Yoshinari; Iséki, Kiyoshi; Tanaka, Shôtarô (1966), "Characterizations of BCI, BCK-algebras", Proc. Japan Acad. 42 (2): 105–107, doi:10.3792/pja/1195522126, MR0202572, http://projecteuclid.org/euclid.pja/1195522126
- Hoo, C.S. (2001), "BCH algebra", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1556080104, http://www.encyclopediaofmath.org/index.php?title=B/b110170
- Hoo, C.S. (2001), "BCI algebra", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1556080104, http://www.encyclopediaofmath.org/index.php?title=B/b110180
- Hoo, C.S. (2001), "BCK algebra", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1556080104, http://www.encyclopediaofmath.org/index.php?title=B/b110190
- Iséki, K.; Tanaka, S. (1978), "An introduction to the theory of BCK-algebras"", Math. Japon. 23: 1–26
- Y. Huang, BCI-algebra, Science Press, Beijing, 2006.
- Imai, Y.; Iséki, K (1966), "On axiom systems of propositional calculi, XIV", Proc. Japan Acad. Ser. A, Math. Sci. 42: 19–22, doi:10.3792/pja/1195522169, http://projecteuclid.org/euclid.pja/1195522169
- Iséki, K. (1966), "An algebra related with a propositional calculus", Proc. Japan Acad. Ser. A, Math. Sci. 42: 26–29, doi:10.3792/pja/1195522171, http://projecteuclid.org/euclid.pja/1195522171